Математичні парадокси та софізми
У своєму житті ми потребуємо деяких констант або явищ, які не піддаються сумніву: кожного ранку над небокраєм з’являється сонце; мама і тато люблять своїх дітей; ми мислимо, отже існуємо; два плюс два дорівнює чотири… Стоп! Щодо останнього твердження математики можуть заперечити й поцікавитись: “А за якою системою числення ми рахуємо?” Тож поговоримо про математичні парадокси та софізми.
Зміст
В трійковій системі числення 2+2 = 11, в четвірковій – 2+2 = 10. Виявляється, що навіть така очевидно проста математична дія може мати різні відповіді. Все залежить від умов. А от 2+2 = 5 – такого немає в жодній системі числення.
Tweet
Інколи більш складні математичні задачі мають вирішення, яке настільки суперечить нашому досвіду, інтуїції і здоровому глузду взагалі, що у це важко повірити, навіть якщо розглянути розв’язок крок за кроком. Такі задачі називаються математичними парадоксами.
Їхні контрего представлені математичними софізмами. Це несподівані твердження, в основу яких закладені малопомітні помилки.
Але не будемо заглиблюватись в теорію і розглянемо найпростіші математичні парадокси і софізми, які мають бути зрозумілими навіть для тих, хто вже зовсім забув шкільний курс з математики.
Парадокс співвідношення парних і натуральних чисел
Дещо все ж нагадаємо. Натуральні числа – це числа, які ми використовуємо при лічбі: 1, 2, 3, 4, 5 і т.д. до нескінченності.
Загадка: парадокс днів народження
Натуральні числа складаються з парних (2, 4, 6 і т.д.) і непарних (1, 3, 5 і т.д.) чисел.
Звідси виникає дуже просте, на перший погляд питання: яких чисел більше – натуральних чи парних?
Відповідь: Логіка підказує нам, що парних чисел рівно удвічі менше, ніж натуральних, оскільки лише кожне друге натуральне число є парним. І це неправильна відповідь! Тому що, кількість парних чисел дорівнює кількості натуральних чисел.
Проілюструємо це у вигляді таблиці, де у верхньому рядку – натуральне число, а у нижньому – відповідне натуральне число, помножене на два.
Оскільки множина натуральних чисел нескінчена, то і ці ряди можна продовжувати до нескінченності: яке б ми не взяли натуральне число, у нього завжди буде свій відповідник з парного числа. Отже, кількість парних чисел дорівнює кількості натуральних.
Парадокс з днями народження
Припустимо, що ви влаштувалися на нову роботу і поки нікого не знаєте. Разом з вами колектив складається з 24 осіб. Як думаєте, яка імовірність того, що як мінімум дві людини святкують день народження в один і той самий день?
Безмежні можливості числа Пі
Відповідь: Інтуїтивно здається, що така імовірність повинна бути малою: врешті решт – у році 365 днів (для спрощення знехтуємо високосними роками), а людей – всього 24. Але насправді імовірність такої події перевищує 50%!
Імовірність того, що дні народження двох людей не співпадуть дорівнює 364/365 (це очевидно, тому що тільки в одному випадку з 365 дні народження співпадають). Імовірність неспівпадіння дня народження третьої особи з першими двома становить 363/365, четвертої – 362/365 і так далі до двадцять четвертої людини, для якої відповідна імовірність дорівнює 342/365. В цілому ми маємо ряд з 23 імовірностей у вигляді дробів.
Щоб знайти імовірність того, що всі 24 дні народженні не співпадають, треба перемножити ці дроби між собою. Після розрахунків скорочуємо дріб і отримуємо 23/50.
Якщо ви азартна людина, то у випадку парі, що серед 24 осіб принаймні у двох співпадуть дні народження, ви будете вигравати у 27 випадках з 50 і програвати у 23 випадках з 50.
Відповідно, чим більша група людей, тим більша імовірність, що у когось співпадуть дні народження. Так, в групі з 30 осіб імовірність такої події перевищує 70%, у групі з 40 осіб – більше 89%, а у групі з 60 осіб – майже дорівнює 100%.
Математика і люди: хто кого створив?
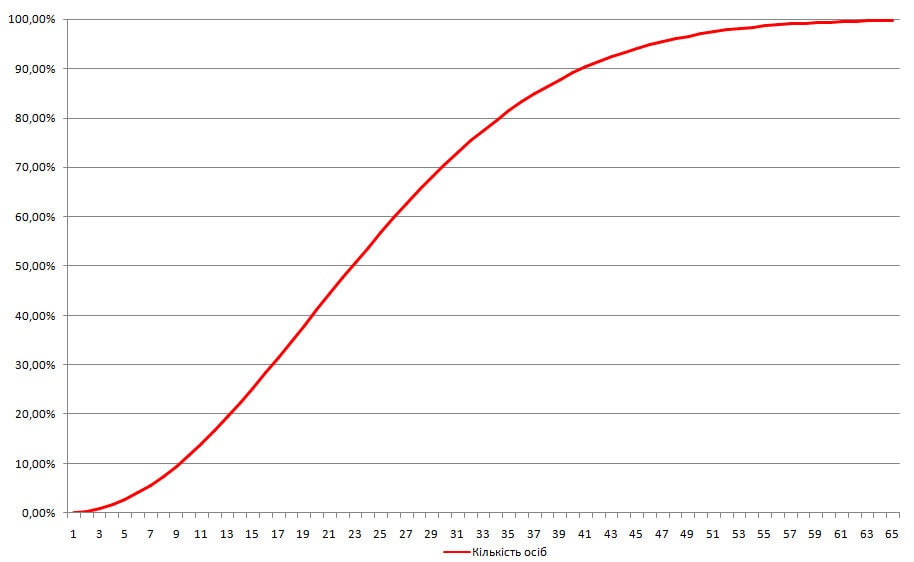
Але не забувайте: якщо хтось народився 29 лютого, то це знижує імовірність збігу днів народження.
Читайте також: Календарний уроборос
Парадокс майже напевної події
Наведений вище графік не повинен вводити вас в оману: майже 100% – це не 100%.
Наприклад, є дві події: імовірність першої – 99%, другої – 99,99%. Імовірності обох майже однакові, обидві події відбуваються майже напевно. Але є нюанс.
Припустимо, що обидві ці події є незалежними (тобто імовірність їх настання не залежить від попередньої події) і можуть відбуватися щодня із своєю імовірністю – відповідно 99% і 99,99%.
Ми можемо розрахувати імовірність того, що обидві події відбуватимуться щодня протягом року.
Для цього нам треба:
- для першої події – піднести імовірність 0,99 до 365 степеня (або перемножити імовірності 0,99 одну на одну 365 разів). Отриманий результат – 0,025 або 2,5%. Тобто імовірність того, що перша подія (імовірність настання якої дорівнює 99%) відбуватиметься щодня протягом року становить лише 2,5%.
- для другої події – піднести імовірність 0,9999 до 365 степеня. Маємо результат – 0,964 або 96,4%. Отже, імовірність того, що друга подія (імовірність настання якої дорівнює 99,99%) відбуватиметься щодня протягом року становить 96,4%.
Здавалось би: невелика різниця імовірностей (всього 0,99%), але вона має суттєве значення.
Парадокс другої дитини
Багатьом відомі анекдотичне питання про імовірність зустріти динозавра на вулиці і відповідь на нього – 50/50 (або зустріну, або – ні).
А якщо трохи ускладнити його? Припустимо, що у пана Парадоксенка двоє дітей. Відомо, що один з них – хлопчик. Яка імовірність, що і друга дитина – теж хлопчик?
Відповідь: теоретичні знання, отримані з анекдоту про динозавра, говорять, що шукана імовірність – 50% (друга дитина – або хлопчик, або дівчинка).
Але насправді простір імовірностей трохи більший. Нехай Х – це хлопчик, Д – дівчинка. Тоді у сім’ї з двома дітьми можливі чотири варіанти – ХХ (два хлопчика), ХД (старший хлопчик, молодша дівчинка), ДХ (старша дівчинка, молодший хлопчик), ДД (дві дівчинки). Ми знаємо, що одна дитина – точно хлопчик. Тоді залишається три варіанти – ХХ, ХД, ДХ. Отже, лише за одного варіанту з трьох у сім’ї росте два хлопчика. Відповідь: імовірність дорівнює 1/3.
Досі сумніваєтесь? І правильно робите. Автор задачі, американський математик і популяризатор науки Мартін Гарднер, і сам не був упевнений у цій відповіді. З умови задачі незрозуміло, як саме ми дізнались про стать одного з дітей. Залежно від цього імовірнісний простір може зрости до 8 варіантів, а імовірність, що друга дитина є хлопчиком – до 50%.
Приклад математичного софізму
Математичний софізм проілюструємо за допомогою мему.
Читайте також: Безмежні можливості числа Пі
Отримуйте сповіщення про нові статті в телеграм-каналі «DAYTODAY». Приєднуйтесь!
Найцікавіше за тиждень
Один лист на тиждень. Без спаму.
Нові статті, добірки та корисні матеріали DAY TODAY — в одному короткому листі.
