Математика і люди: хто кого створив?

Тривалий час у наукових та філософських колах панувала думка, що математика є суто людським винаходом. У цій парадигмі вона сприймається як мова: інструмент, що описує реальні речі, але не існує поза свідомістю тих, хто нею користується. Проте сучасна фізика та філософія дедалі частіше звертаються до альтернативного погляду, коріння якого сягає античної Греції. Піфагорійська школа розглядала реальність як фундаментально математичну структуру. Сьогодні, через дві тисячі років, цей підхід знаходить нове обґрунтування, пропонуючи розглядати математику не як абстракцію, а як невід’ємний компонент природи, що надає структуру фізичному світу.

Зміст

Геометрична ефективність у біології
Арифметика виживання: прості числа та цикади
Філософська дилема: Платон проти Піфагора
Сучасний ренесанс піфагореїзму
Майбутнє наукової парадигми

Геометрична ефективність у біології

Спостереження за живою природою виявляє складні математичні закономірності, які еволюція, здається, “відкрила” задовго до появи людини. Яскравим прикладом є бджолині стільники. Комах цікавить максимальна ефективність: їм необхідно створити комірки для зберігання меду, використовуючи найменшу кількість воску для побудови стінок.

Шестикутник ймовірно є найбільш ефективною формою для замощення площини. Якщо необхідно повністю покрити поверхню плитками однакової форми та розміру, мінімізуючи при цьому загальний периметр, саме шестикутники є ідеальним рішенням. Чарльз Дарвін аргументував це тим, що бджоли еволюціонували, щоб використовувати цю форму, оскільки вона дозволяє створювати найбільші сховища для меду при найменших енергетичних затратах на виробництво воску. Цікаво, що хоча ця гіпотеза була висунута ще в давнину, математично вона була доведена лише у 1999 році математиком Томасом Гейлсом. Це свідчить про те, що комахи “застосовували” складну геометричну теорему за тисячоліття до її формального доведення людством.

Арифметика виживання: прості числа та цикади

Ще більш вражаючий приклад математичної обізнаності природи демонструють північноамериканські періодичні цикади. Існує два підвиди цих комах, які більшу частину життя проводять під землею. Вони виходять на поверхню величезними зграями лише раз на 13 або 17 років (залежно від підвиду) на короткий період близько двох тижнів.

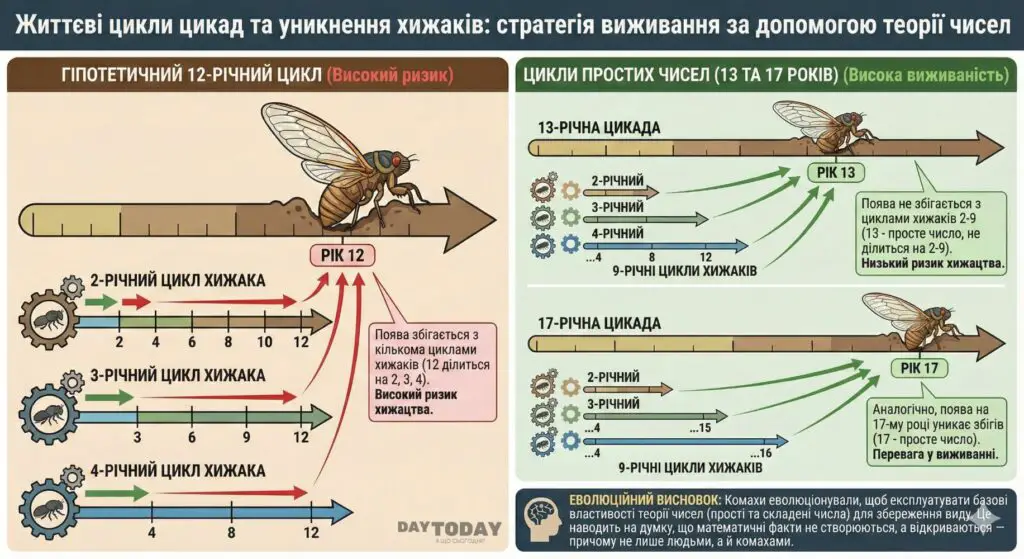
Реклама - Прибрати та підтримати сайт

Вибір саме чисел 13 та 17 не є випадковим. Це прості числа — вони діляться лише на одиницю і на самих себе. Еволюційна логіка тут базується на уникненні хижаків. Припустимо, що у цикад є вороги, які також мають циклічні періоди активності тривалістю 2, 3, 4, 5, 6, 7, 8 або 9 років.

Механізм виживання працює наступним чином:

Якщо життєвий цикл цикади складав би 12 років, то під час виходу на поверхню її зустріли б хижаки з 2, 3 та 4-річними циклами, оскільки 12 ділиться на всі ці числа без залишку.
При циклі у 13 років, жоден із хижаків з циклами від 2 до 9 років не співпаде з виходом цикад, оскільки жодне з цих чисел не ділить 13. Аналогічна логіка стосується і числа 17.

Таким чином, комахи еволюціонували, щоб експлуатувати базові властивості теорії чисел для збереження виду. Це наводить на думку, що математичні факти не створюються, а відкриваються — причому не лише людьми, а й комахами, мильними плівками, чия форма мінімізує поверхневий натяг, та планетарними системами, як-от кільця Сатурна.

Читайте також: Безмежні можливості числа Пі

Філософська дилема: Платон проти Піфагора

Якщо ми погоджуємося з тим, що математика відкривається, а не створюється, виникає питання: що саме ми відкриваємо? Античний філософ Платон вважав, що математика описує об’єкти, які існують реально. До списку платонівських об’єктів належали числа та геометричні фігури. Сьогодні до цього переліку можна додати більш складні сутності: групи, категорії, функції, поля та кільця.

Реклама - Прибрати та підтримати сайт

Проблема платонізму полягає в тому, що ці об’єкти, за його вченням, існують поза простором і часом. Це створює парадокс: якщо математичні об’єкти перебувають в окремому, ізольованому вимірі, як вони можуть пояснювати явища у нашому фізичному світі? Пояснення зазвичай передбачає демонстрацію залежності однієї речі від іншої, але абстракція поза часом і простором не здатна взаємодіяти з матерією.

Тут на сцену виходить піфагореїзм. Стародавні піфагорійці погоджувалися з Платоном, що математика описує світ об’єктів, але відкидали ідею про їхнє існування “поза межами”. Натомість вони стверджували: фізична реальність сама по собі створена з математичних об’єктів, подібно до того, як матерія складається з атомів. Якщо реальність складається з математики, то її роль у поясненні світу стає очевидною і логічною.

Сучасний ренесанс піфагореїзму

У останнє десятиліття ідеї піфагорійців отримали нове життя завдяки роботам провідних фізиків та філософів.

Гіпотеза математичного всесвіту. Космолог Макс Тегмарк стверджує, що реальність є нічим іншим, як одним великим математичним об’єктом. Для ілюстрації цієї ідеї можна згадати концепцію симуляції: комп’ютерна програма, яка створює симуляцію, по суті є математичним об’єктом.
Свідомий всесвіт. Фізик і філософ Джейн Макдоннелл пропонує ще більш радикальний погляд: реальність складається з математичних об’єктів та розуму. У цій моделі математика є інструментом, за допомогою якого Всесвіт, що володіє свідомістю, пізнає сам себе.
Структурний дуалізм. Існує також більш поміркований підхід, який розділяє світ на дві складові: математику та матерію. Математика надає матерії форму, а матерія наповнює математику змістом (субстанцією). У цій парадигмі математичні об’єкти слугують структурним каркасом для фізичного світу.

Майбутнє наукової парадигми

Відродження піфагореїзму у фізиці виглядає закономірним. Протягом останнього століття фізика ставала дедалі більш математизованою, звертаючись до таких абстрактних сфер, як теорія груп та диференціальна геометрія, для пояснення фізичних явищ. Межа між фізикою та математикою поступово розмивається, і стає все важче визначити, які частини світу є фізичними, а які — суто математичними.

Реклама - Прибрати та підтримати сайт

Те, що філософи тривалий час ігнорували піфагореїзм, видається дивним упущенням. Однак наразі ситуація змінюється. Наукова спільнота стоїть на порозі “піфагорійської революції”, яка обіцяє радикально змінити наше розуміння природи реальності, остаточно ствердивши математику не як інструмент опису, а як фундамент буття.

^{За матеріалами публікації на theconversation.com}

Додайте нас в Google News

щоб наші матеріали вам частіше рекомендувалися